Autômatos Finitos Determinísticos

Dentro da Teoria da Computação, uma máquina de estados finitos determinística ou autômato finito determinístico é uma máquina de estados finitos onde, para cada par de estados e símbolo de entrada, existe um próximo estado determinístico.

Formalmente defini-se um A.F.D como sendo um sistema formal , onde:

Aqui apresento alguns exemplos:

1)  L={(a,b)+ onde o número de a’s é impar}

2)  L={(0,1)* onde todos os 1,s apareçam consecutivos}

3)  L={w∈(a,b): w inicia-se com a}

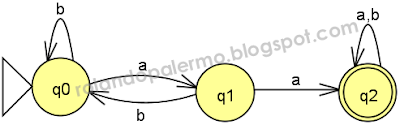
4)  L={w∈(a,b): w contém a substring aa}

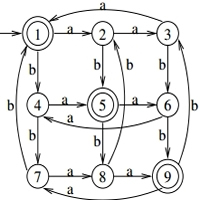
5)  L={w∈(a,b): w contém um número par de 'a' e um número par de 'b'}

6)  L={w∈(a,b,c): w=(abc+)+}

7)  L={w∈(0,1): w não contém 000}

8)  L={w∈(0,1): w contém números iguais de 00 e 11}

9)  L={w∈(0,1): w não contêm os substrings 00 e 11}

10)  L={w∈(0,1): onde todos os 0 são imediatamente precedida e seguida por um 11}

Espero que seja útil isso pra vocês.